Semana 1: La computación#
1.1. Historia de los computadores#
La humanidad, debido a su deseo innato de investigar y resolver problemas, ve la necesidad de hacer cálculos. Desde siglos antes de Cristo el hombre empezó a calcular de forma muy rudimentaria pero eficaz usando los dedos de las manos. Al ver que esta técnica no era suficiente para resolver problemas de cálculos más complejos, en Egipto y China se ideó el ábaco, con el cual se puede realizar sumas y restas. El Ábaco es considerado como el primer dispositivo de cómputo que precedió a la computadora. En 1642 el matemático y filósofo francés Blaise Pascal, pconstruyó una máquina de cálculo mecánica llamada Pascalina. Esta funcionaba con ruedas y engranajes, con el fin de ayudar a su padre en las labores cómo recaudador de impuestos, que le requerían efectuar una gran cantidad cálculos aritméticos cotidianamente. La primera computadora análoga utilizada de manera amplia y extensiva fue la Regla de cálculo inventada en el siglo XVII. Este instrumento de cálculo aritmético permitía hacer cálculos más complejos como potenciación, funciones trigonométricas, logaritmos, entre otros.
Adicional a la necesidad de contar, la humanidad ha requerido registrar y almacenar información. Es así como en ll siglo XX se desarrollaron las primeras computadoras automáticas. Estas hacían posible la aplicación de decisiones lógicas durante el cálculo de los datos; éstas computadoras eran de un tamaño enorme, muy inflexibles, pero con un aumento muy sustancial en la velocidad de procesos de operación.

Imagen 1: reconstrucción de un ábaco romano. Imagen tomada de Wikipedia.

Imagen 2: Pascalina, primera versión de una calculadora. Imagen tomada de Wikipedia.

Imagen 3: Regla de cálculo. Imagen tomada de Wikipedia.
A continuación encontrará una grabación con la explicación del contenido de esta sección.
from IPython.display import YouTubeVideo
YouTubeVideo('39esUGKfXYg')
1.2. Las ciencias de la computación#
Hay problemas grandes y problemas pequeños. Este es un elemento esencial para vivir en sociedad. Aprendemos a clasificar los problemas siendo niños. ¿Cómo clasificar los problemas científicos? Es extremadamente importante para la comunidad científica.
Una manera de clasificar los problemas es entonces preguntarse cuál es el tiempo mínimo le tomaría a una máquina de cómputo resolverlo. Esto se puede hacer usando las siguientes preguntas:
¿Hay problemas que se pueden resolver en una máquina de cómputo si y en otra no?
¿Con qué eficiencia mínima se pueden resolver estos problemas?
¿Todo problema se puede resolver en una máquina de cómputo?
De todas estas preguntas se ocupan científicos de un área que se llama las Ciencias de la Computación.
Las ciencias de la computación, al igual que otras áreas científicas, cuenta con una comunidad que la desarrolla, un objeto de estudio, unos métodos y un cuerpo organizado de resultados.
Para tomar un ejemplo cercano miremos cómo estos elementos se relacionan dentro de una ciencia como la Astronomía. La comunidad de astrónomos estudia los cuerpos celestes utilizando instrumentos como por ejemplo el telescopio y organiza sus resultados en forma de principios, leyes e hipótesis.

Imagen 4: Cúpula del Very Large Telescope en Chile. El apuntador láser indicando que las instalaciones están siendo preparadas para una observación astronómica.
De la misma manera los científicos de la computación estudian la resolución de problemas en una máquina como un objeto abstracto con ayuda de las matemáticas y organiza igualmente sus resultados en forma de principios y teoremas.
La componente teórica de las ciencias de la computación busca determinar qué problemas pueden ser resueltos computacionalmente y con qué eficiencia. Por su parte, la componente aplicada se resuelve preguntas relacionadas con la implementación de las soluciones tales como la arquitectura y los lenguajes de programación.
La teoría de la computación considera distintos modelos de cómputo como por ejemplo los autómatas celulares, las Máquinas de Turing y los computadores cuánticos. A la resolución de un problema en una máquina se la llama un cómputo (o un cálculo) y el objeto que tiene la información que necesita la máquina para realizar el cómputo se llama un algoritmo.
1.3. La computación en la Física y la Astronomía.#
Como aplicación particular, las ciencias de la computación han permitido que áreas como la física y la astronomía se hayan desarrollado de forma exponencial desde mediados del siglo pasado. Particularmente, ha servido para modelar problemas en los cuales:
Se requiere hacer una gran cantidad de cálculos y operaciones aritméticas.
El tiempo de evolución del sistema es muy grande, o muy pequeño.
No hay solución analítica.
A continuación, un ejemplo de cada una de las 3 situaciones expuestas anteriormente.
1.3.1 Interacción gravitacional de una colección de partículas.#
La interacción gravitaciona, descrita por Isaac Newton, tiene una forma matemática que depende de la masa de los dos cuerpos en interacción y de la distancia entre ellos.
Esta ecuación expresa la magnitud de la fuerza en la interacción entre dos partículas de masas \(M\), y \(m\) separadas una distancia \(r\). Y si se revisa,e s un cálculo sencillo de hacer. Sin embargo, cuando en vez de tener solo dos partículas se tiene una colección de N de ellas, el cálculo deja de ser algo que se puede hacer manualmente.
Suponga que tiene 1 mol de partículas de gas y que quiere calcular la fuerza gravitacional sobre una partícula del sistema. Para ello, sabiendo que en 1 mol de cualquier material hay \(10^{23}\) partículas, el total de cálculos a realizar es del orden de:
Si suponemos que somos bastante habilidosos con la calculadora y el lápiz, y tardamos 1 segundo por cálculo, el totald e tiempo que tendríamos que destinar sería del orden de \(10^{38}\) años. Es decir, tardaríamos 27 órdenes de magnitud más que lo que lleva el universo expandiéndose, haciendo imposible realizar todos los cálculos.
Imagen 5: Representación de un sistema de partículas en movimiento
1.3.2 Distribución de materia en el Universo.#
El Universo como lo conocemos, lleva del orden de 14 mil millones de años en expansión. De un estado muy caliente y denso, en el que la materia estaba homogéneamente distribuida, a la red cósmica que observamos hoy en día con nuestros telescopios.
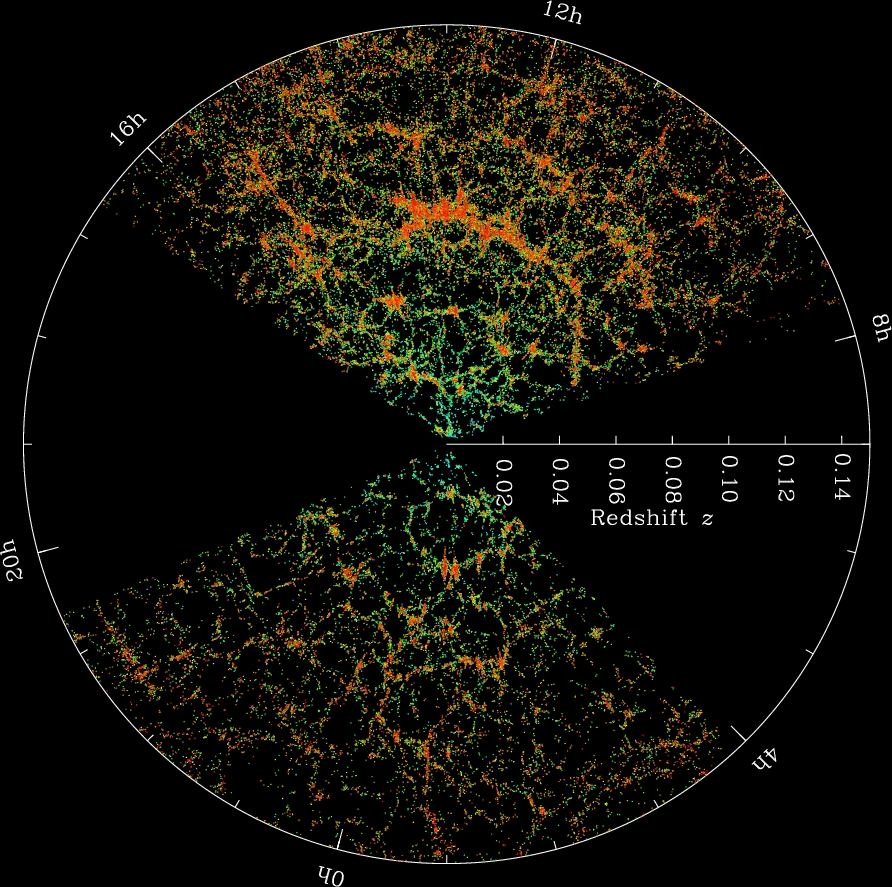
Imagen 6: Distribución de galaxias obtenida con el Sloan Digital Sky Survey. Las galaxias siguen una distribución que parece una malla, conocida como la red cósmica
Seguir y registrar procesos en escalas de tiempo que exceden por tanto lo que llevamos como humanidad (cerca de 10000 años) es entonces físicamente imposible. Sin embargo, al observar la naturaleza del Universo actual y siguiendo las leyes de la física que conocemos, es posible reconstruir los procesos que han debido ocurrir en ese largo intervalo de tiempo. Esto es posible gracias al vertiginoso incremento del poder de cómputo en las últimas décadas
El siguiente vídeo muestra una simulación numérica de la evolución de un conjunto de partículas en el Universo. Los colores indican la densidad de materia, siendo los blancos donde la densidad es mayor y los azules oscuros donde la densidad es menor. Este es el resultado de las simulaciones cosmológicas TNG100-1 e Illustris-1.
from IPython.display import YouTubeVideo
YouTubeVideo('lLbe07XdzKo')
1.3.3 El problema de los N-cuerpos.#
Otro problema que involucra las interacciones gravitacionales es el problema de los N-cuerpos.
Este problema plantea que si bien es posible conocer una solución general para la posición y la velocidad de un par de cuerpos interactuantes, esto no es posible para sistemas con 3 o más cuerpos. Esta imposibilidad recae sobre el hecho de que en sistemas de N-cuerpos (con N\(\geq 3\)), se tienen más variables que ecuaciones disponibles, haciendo del sistema insoluble analíticamente.
Esto, además conlleva a que numérciamente se puedan obtener infinitas soluciones, dificultando la predección sobre cómo evolucionará el sistema gravitacional. Un pequeño cambio en las condiciones iniciales y el sistema puede evolucionar de forma completamente diferente.

