Semana 10: Arreglos de NumPy#
Numpy (Numerical Python)
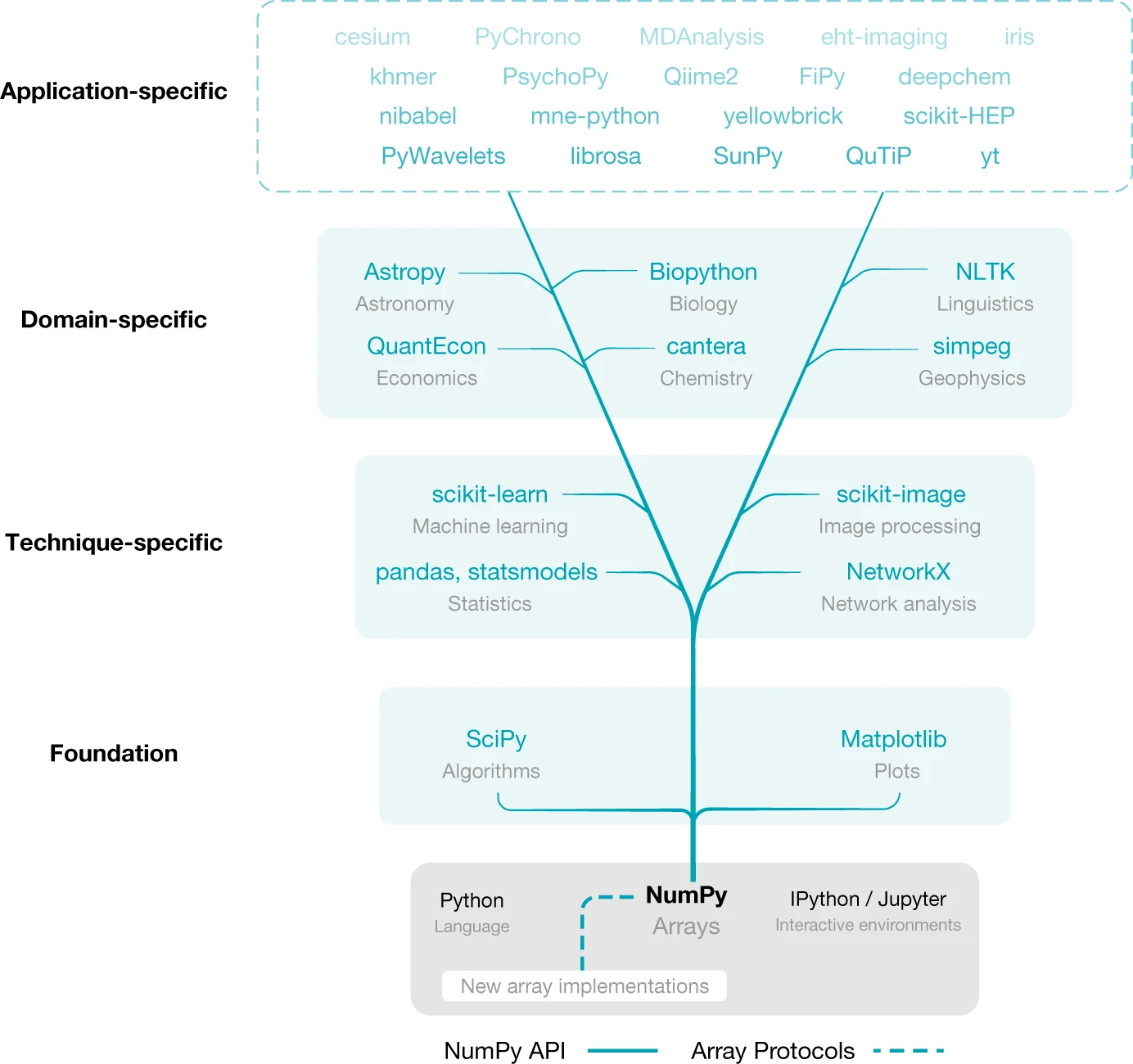
Numpy es la librería fundamental para la computación científica de alto rendimiento y el análisis de datos. Es una libreria que proporciona herramientas para la generación de arreglos y una variedad de funcionalidades para realizar operaciones sobre estos. Numpy se utiliza como bloque básico para una gran cantidad de librerías científicas y de análisis de datos. Dentro de sus utilidades y ventajas, sobresale porque:
Contiene Funciones, módulos, clases que permiten el manejo de arreglos multidimensionales.
Contiene Funciones sofisticadas y optimizadas de math: trigonometicas, random o aleatorias.
Permite incorporar códigos en C/C++ o Fortran.
Por compatibilidad: contiene un paquete de álgebra lineal y permite hacer algo de cálculos estadísticos, ajustes de curvas e interpolación entre otros.
10.1. Definición#
En el núcleo de Numpy, está el objeto ndarray (n-dimensional array). Este encapsula arreglos n-dimensionales de tipos de datos homogéneos, con muchas operaciones que se realizan en código compilado, con lo cual se mejora el rendimiento significativamente.
Por convención, la librería Numpy se import con el alias np:
#Es necesario ejecutar esta celda para llamar a numpy y sus funciones
import numpy as np
Podemos construir un arreglo, por ejemplo, a partir de una lista de Python, mediante el constructor np.array():
# arreglo unidimensional a partir de una lista preexistente
lista = [1, 2, 3, 4]
arreglo = np.array(lista)
arreglo
array([1, 2, 3, 4])
# Verificamos el tipo de las estructuras
print(type(arreglo), type(lista))
<class 'numpy.ndarray'> <class 'list'>
# arreglo bidimensional
lista = [[1, 2,3],[4, 5],['a','b']]
x = np.array([ [1,2,3],[4,5,6],[7,8,9],[10,11,12] ])
x
#, [[1,2,3],[4,5,6],[7,8,9],[10,11,12]]
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
La siguiente imagen ilustra los arreglos de Numpy de una, dos y tres dimensiones. Note que cada dimensión se asocia a un eje (axis). El arreglo unidimensional se asocia a un único eje (axis 0). En el arreglo bidimensional la primera dimensión (filas) se asocia al eje 0 (axis 0), mientras que la segunda dimensión (columnas) se asocia al eje 1 (axis 1).

El arreglo de Numpy contiene una serie de atributos y métodos que definen su estructura. Veamos algunos de los atributos más importantes de este objeto:
10.1.1. dtype#
Este determina el tipo de dato de cada elemento del arreglo. El sistema predeterminado de dtypes que proporciona Numpy es más preciso y más amplio para los tipos básicos que el sistema de tipos que implementa Python

# tipo de dato contenido en el arreglo
x.dtype
dtype('int64')
# Tipo de estructura
type(x)
numpy.ndarray
Podemos definir el tipo de dato a la hora de la creación del arreglo utilizando el kwarg (argumento de teclado) dtype
x1 = np.array([1, 2, 3, 4], dtype='int16') #Crea el arreglo pero yo le especifico
#el tipo de dato que va a almacenar.
x1.dtype
dtype('int16')
o modificarlo posteriormente con el método astype
x1 = x1.astype("int32")
x1
array([1, 2, 3, 4], dtype=int32)
10.1.2. ndim y size:#
La dimensión y el número de elementos del arreglo se pueden obtener mediante los atributos ndim y size, respectivamente
# dimension del arreglo
x1.ndim
1
x2 = np.array([[1,2,3,4],[1,2,3,4]])
x2.ndim
2
x2
array([[1, 2, 3, 4],
[1, 2, 3, 4]])
# numero de elementos del arreglo
x1.size
4
x2.size
8
10.1.3. shape#
Tupla de enteros que representa el rango a lo largo de cada dimensión de los arreglos \(n\)-dimensionales.
# forma del arreglo
x2.shape
(2, 4)
x2
array([[1, 2, 3, 4],
[1, 2, 3, 4]])
Podemos modificar la forma del arreglo modificando el atributo shape directamente
# modificar la forma del arreglo
x1 = np.array([[1,2,3,4],[1,2,3,4]])
print(x1.size)
x1.shape = (4,2)
x1
8
array([[1, 2],
[3, 4],
[1, 2],
[3, 4]])
10.1.4. Traspuesta#
x1.T
array([[1, 3, 1, 3],
[2, 4, 2, 4]])
10.1.5. reshape#
Alternativamente, Numpy proporciona el método reshape, con el cual podemos cambiar la forma de un arreglo. Este toma como argumento el arreglo a modificar y un entero o tupla que represente la nueva forma. Esta nueva forma debe ser compatible con el número de elementos que tenga el arreglo.
# modificar la forma del arreglo
x2 = x2.reshape(2, 4)
x2
array([[1, 2, 3, 4],
[1, 2, 3, 4]])
x2.reshape(2, 2)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Input In [21], in <cell line: 1>()
----> 1 x2.reshape(2, 2)
ValueError: cannot reshape array of size 8 into shape (2,2)
Podemos pasar una de las dimensiones como -1. De esta manera, Numpy se encargará de que el rango en esa dimensión sea compatible con el arreglo original y con el rango de la dimensión que se fijó:
# modificar la forma del arreglo fijando el numero de filas
x2.reshape(-1,8)
array([[1, 2, 3, 4, 1, 2, 3, 4]])
# modificar la forma del arreglo fijando el numero de columnas
x2.reshape(-1, 2)
array([[1, 2],
[3, 4],
[1, 2],
[3, 4]])
10.2. Formas alternativas de construir arreglos#
Numpy proporciona formas alternativas de crear arreglos
10.2.1. np.arange#
np.arange() toma un inicio, final y un paso como la función range() de Python, excepto que devuelve un ndarray y que el paso puede ser un número real. Su sintáxis es de la forma:
np.arange(inicio, final, paso)
list(range(1, 10, 2))
[1, 3, 5, 7, 9]
# arreglo de 1 a 9 con paso 2
x = np.arange(1,10, 2)
x
array([1, 3, 5, 7, 9])
# arreglo de 1 a 9 con paso 1.5
np.arange(1, 10, 0.5)
array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. ,
7.5, 8. , 8.5, 9. , 9.5])
10.2.2. np.linspace#
np.linspace() crea una serie de puntos uniformemente entre un límite inferior y superior que incluye ambos extremos. Su sintáxis es de la forma:
np.linspace(inicio, final, numero de puntos)
# arreglo de -1 a 1 con 10 puntos
x = np.linspace(-1, 1, 10)
x
array([ 5., 10., 15., 20., 25., 30., 35., 40., 45., 50.])
Por defecto se utilizan 50 puntos:
np.linspace(-1, 1)
array([-1. , -0.95918367, -0.91836735, -0.87755102, -0.83673469,
-0.79591837, -0.75510204, -0.71428571, -0.67346939, -0.63265306,
-0.59183673, -0.55102041, -0.51020408, -0.46938776, -0.42857143,
-0.3877551 , -0.34693878, -0.30612245, -0.26530612, -0.2244898 ,
-0.18367347, -0.14285714, -0.10204082, -0.06122449, -0.02040816,
0.02040816, 0.06122449, 0.10204082, 0.14285714, 0.18367347,
0.2244898 , 0.26530612, 0.30612245, 0.34693878, 0.3877551 ,
0.42857143, 0.46938776, 0.51020408, 0.55102041, 0.59183673,
0.63265306, 0.67346939, 0.71428571, 0.75510204, 0.79591837,
0.83673469, 0.87755102, 0.91836735, 0.95918367, 1. ])
10.2.3. np.zeros y np.ones#
Las funciones np.zeros() y np.ones() toman un entero o una tupla de enteros como argumento y devuelven un ndarray cuya forma coincide con la de la tupla y cuyos elementos son cero o uno:
# arreglo de forma (2, 2) llenado con ceros
np.zeros((2,2))
array([[0., 0.],
[0., 0.]])
# arreglo de forma (5,) llenado con unos
np.ones((5,))
array([1., 1., 1., 1., 1.])
10.2.4. np.full#
np.full() funciona de manera similar a zeros() y ones(), solo que podemos llenar el arreglo con cualquier valor:
# arreglo de forma (2, 2) llenado con pi
np.full(shape=(2, 2),fill_value=np.pi)
array([[3.14159265, 3.14159265],
[3.14159265, 3.14159265]])
10.2.5. Arreglos aleatorios#
En muchas ocaciones vamos a necesitar construir arreglos cuyos elementos se generen de forma aleatoria. En estos casos podemos utilizar el submódulo random de la librería.
La función np.random.rand() genera un arreglo cuyos elementos se muestrean de una distribución uniforme en el intervalo (0, 1).
np.random.rand(shape)
# arreglo "aleatorio" de forma (3, 3) con numeros de punto flotante en el intervalo (0, 1)
np.random.rand(3, 3)
array([[0.89141192, 0.02420299, 0.50321879],
[0.40018415, 0.68042353, 0.56103391],
[0.66104633, 0.02304592, 0.89206359]])
np.random.rand(3, 5)
array([[0.28467079, 0.90458932, 0.16517301, 0.20994743, 0.23846211],
[0.97429477, 0.12278936, 0.33781405, 0.98439667, 0.1499058 ],
[0.873485 , 0.6591112 , 0.10817036, 0.57867571, 0.30477634]])
La función np.random.randint() genera un arreglo aleatorio de números enteros en un rango especifico con una forma dada:
np.random.randint(limite_inferior, limite_superior, shape)
# arreglo aleatorio de forma (2, 2) con numeros enteros en el intervalo (10, 20)
np.random.randint(10, 20, (2, 2))
array([[18, 19],
[11, 17]])
# definicion de la semilla para la generacion
# de los numeros pseudoaleatorios
np.random.seed(20)
np.random.randint(10, 20, (2, 2))
array([[13, 19],
[14, 16]])
Ejercicio 1: Crear un arreglo 3x3 con valores comprendidos entre 2 y 10 (secuencialmente)
np.random.randint(2, 10, (3,3))
array([[5, 5, 9],
[8, 7, 7],
[8, 7, 4]])
np.arange(2, 11).reshape(3, 3)
array([[ 2, 3, 4],
[ 5, 6, 7],
[ 8, 9, 10]])
Ejercicio 2: Crear un arreglo aleatorio de 3x3 y luego conviertalo a un arreglo unidimensional (utilice los métodos reshape() o flatten())
x = np.random.randint(2, 10, (3, 3))
x
array([[3, 9, 5],
[3, 7, 7],
[7, 3, 5]])
x.reshape(x.size,)
array([3, 9, 5, 3, 7, 7, 7, 3, 5])
# con reshape
x.reshape(-1)
array([3, 9, 5, 3, 7, 7, 7, 3, 5])
# con flatten
x.flatten()
array([3, 9, 5, 3, 7, 7, 7, 3, 5])
10.3. Funciones universales#
De los ejemplos anteriores vemos que cuando los arreglos son de Numpy, se está realizando lo que se conoce como una operación vectorizada, la cual es una operación sobre los arreglos que se realiza elemento a elemento, mediante lo que conocemos como funciones universales (ufuncs) de Numpy. La siguiente tabla nos muestra algunas de las funciones universales disponibles en Numpy (ver documentación)

x = np.linspace(0,10,5)
y = np.full(shape=(1,5), fill_value = np.e)
z = x+y
z = np.power(x,y)
z
array([[ 0. , 12.07016187, 79.43235917, 239.14600544,
522.73529967]])
También podemos utilizar ufuncs como las funciones trigonométricas, exponencial y logaritmo
np.sin(x)
array([-0.95892427, -0.54402111, 0.65028784, 0.91294525, -0.13235175,
-0.98803162, -0.42818267, 0.74511316, 0.85090352, -0.26237485])
coseno = np.cos(x)
coseno
array([ 0.28366219, -0.83907153, -0.75968791, 0.40808206, 0.99120281,
0.15425145, -0.90369221, -0.66693806, 0.52532199, 0.96496603])
np.tan(x)
np.tanh()
np.sec()
np.csc()
10.4. Indexación#
Los arreglos de Numpy tienen el mismo esquema de indexación de las listas de Python. La diferencia es que, al ser objetos n-dimensionales, podemos indexar cada dimensión de forma independiente. Podemos pasar una tupla donde el primer elemento corresponde a la indexación que queremos implementar sobre las filas, mientras que el segundo corresponde a la selección de las columnas:
Ejemplo: Dada la lista
[[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
lista = [[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
arreglo = np.array(lista)
seleccionar la primera fila
# lista
lista[0][1]
1
# arreglo
arreglo[:,2]
array([0, 1, 2])
seleccionar la primera columna
arreglo[:, 0]
array([0, 3, 6])
seleccionar el elemento de la ultima fila y ultima columna
# arreglo
arreglo[-1, -1]
8
seleccionar desde la segunda fila y todas las columnas
arreglo
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
# arreglo
arreglo[1:,0]
array([3, 6])
Ejemplo: Crear un arreglo 4x4 con unos en el borde y ceros en el centro
ones = np.ones((4,4))
ones
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
ones[1:3, 1:3] = 0 # [[0, 0],[0, 0]]
ones
array([[1., 1., 1., 1.],
[1., 0., 0., 1.],
[1., 0., 0., 1.],
[1., 1., 1., 1.]])
Ejemplo 4: Crear un arreglo 8x8 que tenga el patrón de un tablero de ajedrez con unos y ceros
import numpy as np
ones = np.ones((8, 8))
ones
array([[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.]])
ones[::2, ::2] = 0
ones[1::2, 1::2] = 0
ones
array([[0., 1., 0., 1., 0., 1., 0., 1.],
[1., 0., 1., 0., 1., 0., 1., 0.],
[0., 1., 0., 1., 0., 1., 0., 1.],
[1., 0., 1., 0., 1., 0., 1., 0.],
[0., 1., 0., 1., 0., 1., 0., 1.],
[1., 0., 1., 0., 1., 0., 1., 0.],
[0., 1., 0., 1., 0., 1., 0., 1.],
[1., 0., 1., 0., 1., 0., 1., 0.]])
Numpy contiene funciones y métodos para una gran variedad de tareas
Ejemplo: Dada la lista
[[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
Seleccione los elementos de la diagonal
lista = [[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
lista[0][0], lista[1][1], lista[2][2]
(0, 4, 8)
# np.diag
np.diag(lista)
array([0, 4, 8])
Ejemplo: Escriba un programa para encontrar los valores comunes entre las listas
[0, 10, 20, 40, 60]
[10, 30, 40]
# intersect1d
a = [0, 10, 20, 40, 60]
b = [10, 30, 40]
np.intersect1d(a, b)
array([10, 40])
Ejemplo: Escriba un programa para encontrar los valores de un arreglo a que no estén presentes en otro arreglo b
a = [0, 10, 20, 40, 60, 80]
b = [10, 30, 40, 50, 70]
# np.setdiff1d
a = [0, 10, 20, 40, 60, 80]
b = [10, 30, 40, 50, 70]
np.setdiff1d(a, b)
array([ 0, 20, 60, 80])
Ejemplo: Escriba un programa para comprobar si cada elemento de un arreglo unidimensional a está presente en un segundo arreglo b
a = np.array([0, 10, 20, 40, 60])
b = np.array([0, 40])
# np.in1d
a = np.array([0, 10, 20, 40, 60])
b = np.array([0, 40])
# valores de a que estan en b
np.in1d(a, b)
array([ True, False, False, True, False])
# valores de b que estan en a
np.in1d(b,a)
array([ True, True])
Acá puede encontrar ejercicios adicionales relacionados con el objeto np.ndarray
