Semana 11: Graficación con Matplotlib

Semana 11: Graficación con Matplotlib#

11.1. Definición#

Matplotlib es una herramienta para visualización de datos en Python, construida sobre arreglos de NumPy. Una visualización típica es de la siguiente forma:

Figure:

Axes:

Gráfica:

En resumen, la figura puede considerarse como un contenedor único que contiene todos los objetos que representan los ejes, gráficos y etiquetas. Por otra parte, el conjunto de ejes es un cuadro delimitador con marcas y etiquetas, que eventualmente contendrá los elementos del gráfico que componen nuestra visualización.

11.2. Creando figuras y ejes#

Usaremos el submódulo pyplot para realizar nuestros gráficos. Por convención se utiliza el alias plt

import numpy as np
#import matplotlib
import matplotlib.pyplot as plt

La figura y los ejes se suelen referenciar mediante los nombres de variables fig y ax, respectivamente. Estos se pueden obtener mediante la función subplots

# figura y conjunto de ejes
figura, ejes = plt.subplots()
_images/acf8b18dcf2c5918dca86ee7dd477a1e58f3bc043cdd9a261c9cab3c24addebd.png

A través de los métodos y atributos de estos objetos personalizaremos la visualización. (Puede consultar todos los atributos y métodos de la clase axes en este link).

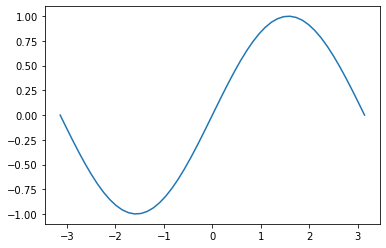
Por ejemplo, con el método ax.plot() construimos un gráfico de línea

Enlace a las funciones y atributos de numpy: link

# arreglos a graficar
angulos = np.linspace(-np.pi, np.pi)
sen = np.sin(angulos)

# se crean la figura y los ejes
figura, ejes = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ejes.plot(angulos,sen)

[<matplotlib.lines.Line2D at 0x7f461333e9a0>]
_images/7597e7a6d67638986c573abb0e21b84628782b88f741184407b6d6f4eb6a732c.png 
x = np.linspace(-np.pi, np.pi)
len(x)
x

array([-3.14159265, -3.01336438, -2.88513611, -2.75690784, -2.62867957,
       -2.5004513 , -2.37222302, -2.24399475, -2.11576648, -1.98753821,
       -1.85930994, -1.73108167, -1.60285339, -1.47462512, -1.34639685,
       -1.21816858, -1.08994031, -0.96171204, -0.83348377, -0.70525549,
       -0.57702722, -0.44879895, -0.32057068, -0.19234241, -0.06411414,
        0.06411414,  0.19234241,  0.32057068,  0.44879895,  0.57702722,
        0.70525549,  0.83348377,  0.96171204,  1.08994031,  1.21816858,
        1.34639685,  1.47462512,  1.60285339,  1.73108167,  1.85930994,
        1.98753821,  2.11576648,  2.24399475,  2.37222302,  2.5004513 ,
        2.62867957,  2.75690784,  2.88513611,  3.01336438,  3.14159265])

11.3. Personalización básica del gráfico#

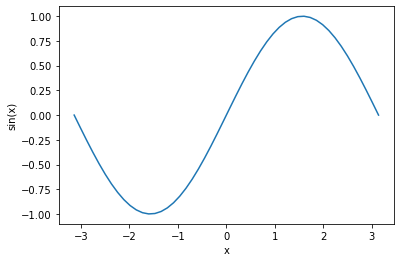
Título y etiquetas de los ejes: Podemos agregar al gráfico un título y etiquetas para los ejes \(x\) y \(y\), con los métodos set_title, set_xlabel y set_ylabel, respectivamente:

LaTeX

sin(x)

\(\sin(x)\)

\(\rho\)

\(\frac{1}{2}\)

\(\sum_{i=0}^{i=N} A_i\)

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y)

# agregar etiquetas de los ejes
#ax.set_xlabel("$x$")
#ax.set_ylabel("$\sin(x)$")

ax.set_xlabel('x')
ax.set_ylabel('sin(x)')

Text(0, 0.5, 'sin(x)')
_images/8a71626b26a7e010d9f26f99eca1c7b844090f62ff5b3318c44a2d9e4d923ac4.png 
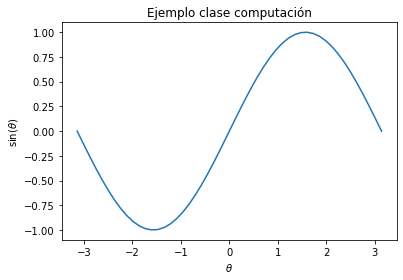
# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y)

# agregar etiquetas de los ejes
ax.set_xlabel("$\\theta$")
ax.set_ylabel("$\\sin(\\theta)$")

# agregar titulo
ax.set_title("Ejemplo clase computación")

Text(0.5, 1.0, 'Ejemplo clase computación')
_images/3b16b15c2f54066c841d3558c784a0329a0292f42adf880342fd685dfdeab0cd.png

Leyenda: Para agregar una leyenda a la gráfica, utilizamos el kwarg label de ax.plot. Para que la leyenda se muestre debemos ejecutar el método ax.legend

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y, label="curva 1")

# agregar etiquetas de los ejes
ax.set_xlabel("$x$")
ax.set_ylabel("$\sin(x)$")

# agregar titulo
ax.set_title("Funcion Seno")

# agregar leyenda
ax.legend(title='Funciones');
_images/7a67561a014243a3d3b79d1969f7f32238345de0aa6608d1b04802a999705834.png

En el estilo orientado a objetos, en lugar de llamar las funciones que contienen el prefijo set individualmente, es más conveniente usar el método ax.set() para establecer todas estas propiedades a la vez:

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y, label="sin")

# agregar etiquetas de los ejes y titulo
ax.set(
    xlabel="x",
    ylabel="sin(x)",
    title="Funcion seno",
)

# agregar leyenda
ax.legend(title="Funciones trigonometricas")

<matplotlib.legend.Legend at 0x7f4613079730>
_images/bf5aec5574602ae96710417f1e491893f724b092d6649c64d36316c0095b43f6.png

Tamaño de la figura: Podemos modificar el tamaño de la figura utilizando el argumento por palabra clave figsize (en el cual debemos definir una tupla que corresponde al tamaño en \(x\) y en \(y\) de la figura) en la función subplots

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes (modificar el tamaño de la figura)
# figsize=(tamaño de ancho, tamaño del alto) [pulgadas]
fig, ax = plt.subplots(figsize=(6,4))

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y, label="sin")

# agregar etiquetas de los ejes y titulo
ax.set(
    xlabel="x",
    ylabel="sin(x)",
    title="Funcion seno",
)

# agregar leyenda
ax.legend(title="Funciones trigonometricas");
_images/bf5aec5574602ae96710417f1e491893f724b092d6649c64d36316c0095b43f6.png

Si queremos definir el tamaño de la figura de forma global, podemos utilizar plt.rcParams["figure.figsize"]

plt.rcParams["figure.figsize"] = (6, 4)

11.4. Cambiando el estilo de graficación#

Ya vimos el estilo de graficación estándar que se tiene en matplotlib.pyplot. Una personalización del fondo (y otras características del gráfico) requiere la especificación de la figura. Sin embargo, podemos utilizar la directiva plt.style para elegir diferentes estilos para las visualizaciones. Mediante el atributo plt.style.available podemos acceder a los diferentes estilos disponibles:

plt.style.available

['Solarize_Light2',
 '_classic_test_patch',
 '_mpl-gallery',
 '_mpl-gallery-nogrid',
 'bmh',
 'classic',
 'dark_background',
 'fast',
 'fivethirtyeight',
 'ggplot',
 'grayscale',
 'seaborn',
 'seaborn-bright',
 'seaborn-colorblind',
 'seaborn-dark',
 'seaborn-dark-palette',
 'seaborn-darkgrid',
 'seaborn-deep',
 'seaborn-muted',
 'seaborn-notebook',
 'seaborn-paper',
 'seaborn-pastel',
 'seaborn-poster',
 'seaborn-talk',
 'seaborn-ticks',
 'seaborn-white',
 'seaborn-whitegrid',
 'tableau-colorblind10']

Podemos elegir alguno de estos estilos utilizando el método plt.style.use:

plt.style.use('tableau-colorblind10')

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)
y = np.sin(x)

# se crean la figura y los ejes (modificar el tamaño de la figura)
# figsize=(tamaño de ancho, tamaño del alto) [pulgadas]
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, y,label="sin", marker = "*" )

# agregar etiquetas de los ejes y titulo
ax.set(
    xlabel="x",
    ylabel="sin(x)",
    title="Funcion seno",
)

# agregar leyenda
ax.legend(title="Funciones trigonometricas");
_images/4479ef4ebfc5ed95e0215a9352fc7aaf291faf1a320bea9825e4bd47a893b843.png

Configurando marker podemos establecer la forma que queremos que tenga el punto en la gráfica, consulte la documentación de matplotlib para más marcadores.

11.5. Creando mútiples gráficos#

Para la generación de la figura y de uno o más conjuntos de ejes podemos recurrir a la función plt.subplots, la cual crea estos objetos y devuelve una referencia a la figura y al conjunto de ejes (si solo se ha creado uno) o a una lista de referencias a los conjuntos de ejes (si se han creado dos o más).

Gráficos en una figura y un conjunto de ejes

Como ya vimos, la función plt.subplots crea por defecto una figura y un solo eje. Para tener dos gráficos en el mismo eje utilizamos la función plot reiteradamente:

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)

# se crean la figura y los ejes (modificar el tamaño de la figura)
# figsize=(tamaño de ancho, tamaño del alto) [pulgadas]
fig, ax = plt.subplots()

# se realiza la grafica mediante la referencia al conjunto de ejes
ax.plot(x, np.sin(x), label="sin", color='r', linestyle="-.")
ax.plot(x, np.cos(x), label="cos", linestyle=":")
ax.plot(x,np.tanh(x), label="tanh", linestyle="--")

# agregar etiquetas de los ejes y titulo
ax.set(xlabel="x",)

# agregar leyenda
ax.legend(title="Funciones trigonometricas");
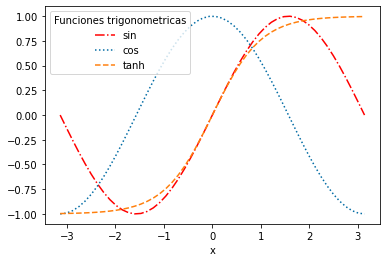
_images/7f063d9c1e671f7a4f539699e272ac38f1bc0166e1e8091cb8f722fdbf25dffc.png

El estilo de las líneas se especifica con linestyle:

  • “-” o “solid”: línea sólida (es la opción por defecto).

  • “–” o “dashed”: línea discontinua.

  • “-.” o “dashdot”: línea que alterna guiones y puntos.

  • “:” o “dotted”: línea de puntos.

  • “None”, “ “ o “”: no muestra nada.

Gráficos en una figura y múltiples conjuntos de ejes

Si queremos especificar el número de ejes a usar, debemos hacerlo explícitamente en la función plt.subplots. Sus dos primeros argumentos representan el número de filas y columnas a utilizar

# tipo y forma de una figura 1x2
fig, ax = plt.subplots(3, 2)

print(type(ax))
#print(ax.shape)

<class 'numpy.ndarray'>
_images/2ece3a1c3a9a60c67bbcc3978a13a4f02a44723026a57c24d316b131ce624da7.png 
ax[1]

array([<AxesSubplot:>, <AxesSubplot:>], dtype=object)

Para pintar una gráfica en alguno de estos conjuntos de ejes simplemente debemos referenciar el eje mediante el elemento de ax correspondiente:

# arreglos a graficar
x = np.linspace(-np.pi, np.pi)

# se crean la figura y los ejes (modificar el tamaño de la figura)
# figsize=(tamaño de ancho, tamaño del alto) [pulgadas]
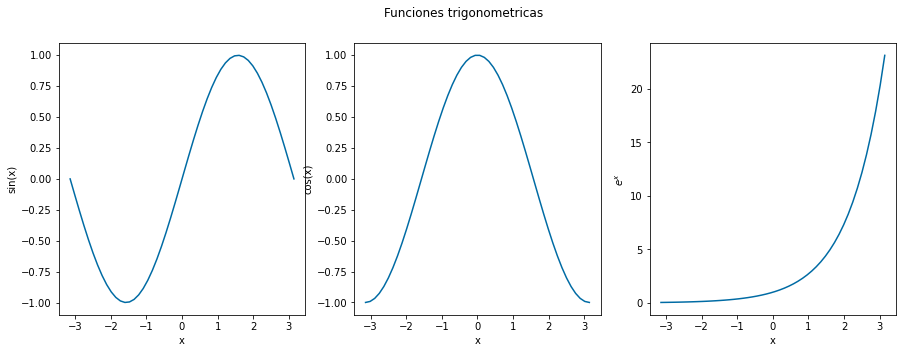
fig, ax = plt.subplots(1, 3, figsize=(15, 5))

# se realiza la grafica mediante la referencia al conjunto de ejes
ax[0].plot(x, np.sin(x))
ax[1].plot(x, np.cos(x))
ax[2].plot(x,np.exp(x))

# agregar etiquetas de los ejes y titulo
ax[0].set(xlabel="x", ylabel="sin(x)")
ax[1].set(xlabel="x", ylabel="cos(x)")
ax[2].set(xlabel='x', ylabel='$e^{x}$')

# titulo de la figura
fig.suptitle("Funciones trigonometricas");
_images/bee6c48e79e27b5fdc418cd8ebda943717ee2680756a505a7c9b9cf0727d88f3.png 
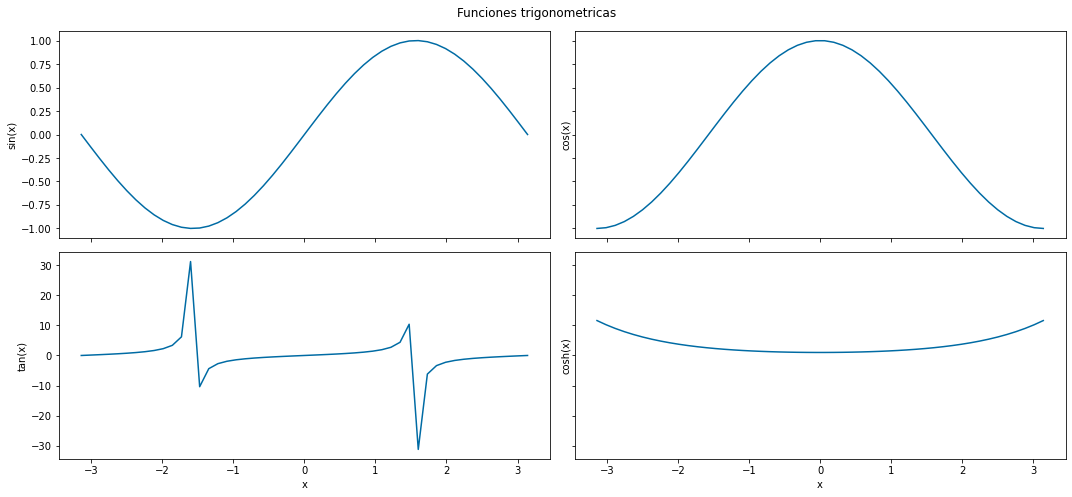
# arreglos a graficar
x = np.linspace(-np.pi, np.pi)

# se crean la figura y los ejes (modificar el tamaño de la figura)
# figsize=(tamaño de ancho, tamaño del alto) [pulgadas]
fig, ax = plt.subplots(
    2, 2,
    figsize=(15, 7),
    tight_layout=True,
    sharex=True,
    sharey="row"
    )

# se realiza la grafica mediante la referencia al conjunto de ejes
ax[0,0].plot(x, np.sin(x))
ax[0,1].plot(x, np.cos(x))
ax[1,0].plot(x, np.tan(x))
ax[1,1].plot(x, np.cosh(x))

# agregar etiquetas de los ejes y titulo
ax[0,0].set(ylabel="sin(x)")
ax[0,1].set(ylabel="cos(x)")
ax[1,0].set(xlabel="x", ylabel="tan(x)")
ax[1,1].set(xlabel="x", ylabel="cosh(x)")

# titulo de la figura
fig.suptitle("Funciones trigonometricas")

fig.savefig("myplot.png")
_images/993dc311150cb9fec4bbf77f5e5eeb43267240e913ceacd05e524cac8ba85334.png

NOTAS:

  • Cuando trabajamos en un notebook, las figuras se muestran de forma automática, como ya hemos visto. Sin embargo, si se escribe el código en un editor de texto, la figura no se mostrará automáticamente sino que debemos ejecutar el comando plt.show() (o fig.show()) para que se genere y se muestre la visualización.

  • Si queremos guardar la visualización, podemos utilizar el comando plt.savefig() (o fig.savefig()), donde debemos especificar la dirección en la que queremos guardar la gráfica y su nombre, además del formato de salida con el argumento por palabra clave format. Si no especificamos este, el formato de salida se infiere del nombre.

    Ejemplo: Guardar la gráfica con el nombre figure en formato png: fig.savefig("figure.png")

11.6. Gráficos en 3D#

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import style

# Creamos la figura
fig = plt.figure()

# Agregamos un plano 3D
ax1 = fig.add_subplot(projection='3d')


# Definimos los datos de prueba
x = [1,2,3,4,5,6,7,8,9,10]
y = [5,6,7,8,2,5,6,3,7,2]
z = [1,2,6,3,2,7,3,3,7,2]

# Datos adicionales
x2 = [-1,-2,-3,-4,-5,-6,-7,-8,-9,-10]
y2 = [-5,-6,-7,-8,-2,-5,-6,-3,-7,-2]
z2 = [1,2,6,3,2,7,3,3,7,2]

# Agregamos los puntos en el plano 3D
ax1.scatter(x, y, z, c='g', marker='.')
ax1.scatter(x2, y2, z2, c ='r', marker='*')


ax1.set_xlabel('Etiqueta del eje X')
ax1.set_ylabel('Etiqueta del eje Y')
ax1.set_zlabel('Etiqueta del eje Z')

Text(0.5, 0, 'Etiqueta del eje Z')
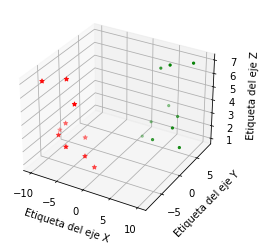
_images/b29a803ccb87d11f77cae091bac04724a98759b18483fed6dc36f1e7faf6b54e.png

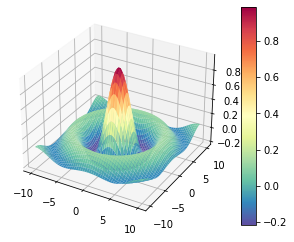
11.7. Gráficos de superficie#

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np

# Datos de muestra
a = 10
X, Y = np.meshgrid(np.linspace(-a,a),
                   np.linspace(-a,a))

Z = np.sin(np.sqrt(X**2 + Y**2))/np.sqrt(X**2 + Y**2)

fig = plt.figure()
ax = fig.add_subplot(projection = '3d')

# Superficie 3D
plot = ax.plot_surface(X, Y, Z, cmap = 'Spectral_r')
fig.colorbar(plot, ax = ax, shrink = 1, aspect = 15)

<matplotlib.colorbar.Colorbar at 0x7f4612a4ee50>
_images/11483531617c2f6989a82f52c57b8dfc424e79a11350078bff8efb57541b6ae4.png
Contents